What kind of solid is this?

In a technical drawing, a solid is represented by parallel projections of its front view, its side view and its top view. The visible edges are shown with solid lines, the invisible ones with dashed lines. If two edges lie on top of each other in the projection, only the solid line is visible, of course.
Can there be a solid whose projections look like the following? If so, what does this solid look like?
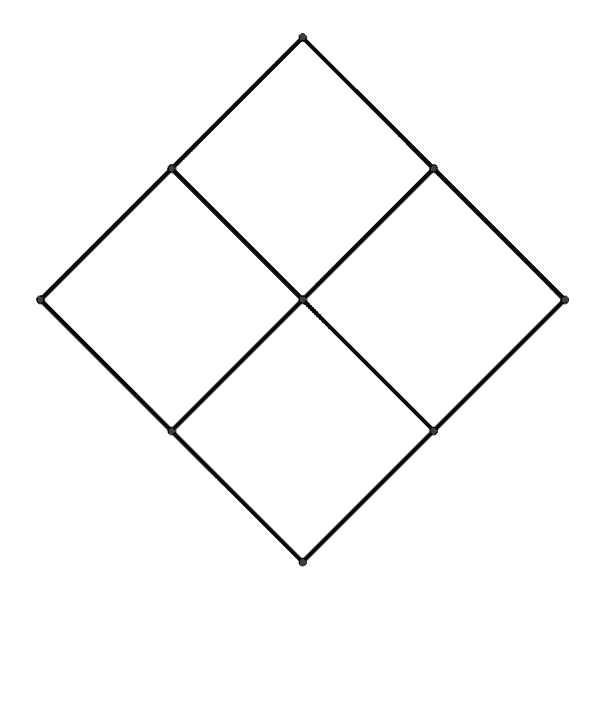


You can find the solution in the box below.
Solution
The projections represent a rhombic dodecahedron. This is a solid figure bounded by twelve congruent equilateral but non-rectangular quadrilaterals. It can be thought of as a cube with six pyramids on top, whose angles of inclination are 45^{\circ}. As a result, two of the triangular pyramid faces meeting at one edge of the cube complement each other to form a rhombus.
In the technical drawing, one looks from above, from the side and from the front at one pyramid top each. The four rhombuses visible in this view are distorted into squares by the projection.
The following applet shows an interactive 3D view of a rhombic dodecahedron. It can be rotated (with the right mouse button pressed), and the slider can be used to set the side, front, and top views.
The following figure shows the mesh of the rhombic dodecahedron:
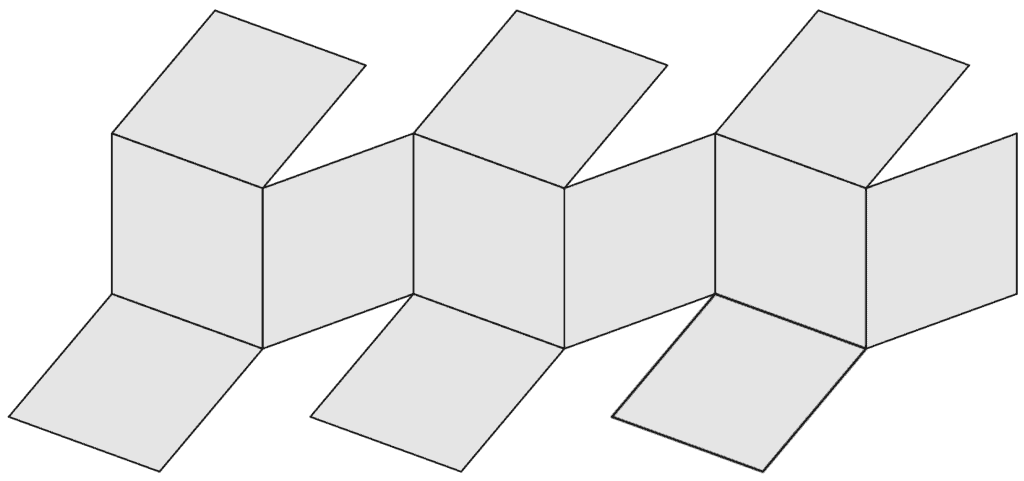
More information about the rhombic dodecahedron can be found on Wikipedia.
Share
If you think this page might be of interest to others then click one of the buttons:






